Для описания климата используют получаемые в результате математической обработки метеорологических рядов различные статистические характеристики. Их называют климатическими показателями. Показателями отдельных метеорологических величин обычно служат: средние значения; крайние (максимальные и минимальные) значения; повторяемость (или вероятность) и накопленная (кумулятивная) повторяемость различных значений элементов; показатели изменчивости; показатели асимметрии и крутости кривой распределения. Все климатические показатели вычисляются по многолетним данным для каждого месяца (сезона) или в целом за год.

Средние значения. В качестве среднего в климатологии чаще всего используется среднее арифметическое значение метеорологического элемента. Оно выражает в виде одного числа наиболее важную часть информации о режиме метеорологических элементов и очень удобно для сопоставления метеоэлементов во времени и пространстве.

Пользуясь средними значениями метеорологических величин, легко сравнивать особенности климатов различных районов, что имеет научное и практическое значение. Это сравнение становится особенно наглядным после нанесения на карту многолетних средних значений метеорологических величин, представленных в виде изолиний.

Кроме того, среднее арифметическое является оценкой параметров многих теоретических распределений и удобно при различных математических расчетах.

Среднее представляет собой сумму значений членов ряда х1, x2, x3 ... xn, деленную на их общее число n:

.

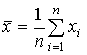Если для вычисления среднего в качестве исходных данных используется сгруппированный метеорологический ряд (статистическое распределение), то применяют формулу:

,

где х_i – срединное значение интервала; m – частота градации; k – число градаций.

Крайние значения. Если бы условия погоды отличались устойчивостью из года в год и изо дня в день, то для характеристики климата было бы достаточно средних данных. Однако характерная черта климата на большей части территории земного шара – это неустойчивость, непостоянство, что и является причиной трудностей при описаниях климата, а также при прогнозах погоды.

В связи с этим в климатологии большое внимание уделяется крайним значениям метеорологических величин. Они указывают на аномалии погодных процессов, учет которых полезен для многих отраслей народного хозяйства. Так, в северной части Черноморского побережья Кавказа в общем достаточно тепла для выращивания цитрусовых культур, но иногда здесь бывают и заморозки, оказывающие губительное влияние на урожай.

Крайние значения температуры и влажности воздуха необходимы для оценки условий хранения различных материалов и оборудования на открытом воздухе. Резкие повышения температуры до нуля в морозные периоды – оттепели – сокращают сроки эксплуатации различных сооружений. Кратковременные ливневые осадки приводят к наводнениям, разрушают наземные пути сообщения. Сильные снегопады и метели создают снегозаносы и нарушают работу наземного транспорта.

Для оценки крайних значений метеорологических величин в климатологии принято определять:

а) абсолютный максимум и абсолютный минимум;

б) средние из абсолютных максимумов или минимумов (средние из годовых экстремальных величин);

в) средние экстремумы за месяц, т.е. средние значения из максимумов и минимумов за сутки.

Абсолютным максимумом (минимумом) называется наивысшее (наинизшее) значение, которое наблюдалось хотя бы один раз в течение рассматриваемого периода.

Крайние значения выбираются из многолетних наблюдений. Выборку можно производить независимо от того, в каком календарном периоде отмечались экстремальные значения на данной станции, или выбирать эти значения только из наблюдений в одноименные календарные периоды (месяцы, сезоны) различных лет. В первом случае мы получаем абсолютный максимум или абсолютный минимум, присущий станции вообще, во втором случае получаем абсолютный максимум или минимум, присущий станции в определенный календарный период. Например, самая низкая температура, которая наблюдалась на ст. Икс с 1891 по 1995 г., была отмечена 12.01.1915 г. и составляла –50 °С. Эта величина является абсолютным минимумом температуры воздуха на ст. Икс за этот ряд лет наблюдений.

Другой пример. Просматривая результаты наблюдений по температуре воздуха на той же станции за июль с 1891–1995 г., отмечаем, что самая низкая температура была отмечена 06.07.1898 г. и составляла 0,4 °С. Эта температура является абсолютным минимумом для июля на ст. Икс.

Так как величины, близкие к абсолютным максимумам и минимумам, наблюдаются редко, то для получения представления о более вероятных низких и высоких значениях температуры вычисляют среднее из экстремальных. Различают средний максимум или средний минимум метеорологических величин и среднее из абсолютных максимумов или минимумов.

Первую характеристику вычисляют как среднее из ежедневных максимальных и минимальных значений, вторую – как среднее из абсолютных максимумов или минимумов, наблюдавшихся за каждый год. Чаще всего в климатологии пользуются средним из абсолютных максимумов (минимумов) по температуре воздуха. Для этого выписывают абсолютный максимум (минимум) за каждый отдельный год и подсчитывают среднее за весь период наблюдений. По крайним значениям метеорологических величин можно судить о климатических контрастах на земном шаре.

Амплитуды. Для решения многих практических вопросов большое значение имеет амплитуда колебаний. В метеорологии и климатологии амплитудой называют разность между максимальным и минимальным значениями метеорологической величины. Если разность вычисляется между абсолютным максимумом и абсолютным минимумом, она называется абсолютной амплитудой.

Разность между наибольшими и наименьшими средними месячными (за ряд лет) значениями метеорологических величин называется годовой амплитудой. Амплитуда, полученная как разность между максимальными и минимальными значениями за сутки, называется суточной амплитудой.

Характеристики изменчивости. Характеристиками изменчивости или рассеивания значений элемента относительно среднего служат среднее абсолютное и среднее квадратическое отклонения и коэффициент вариации.

Для того, чтобы показать, насколько сильно колеблются значения элементов в отдельные годы, вычисляют их среднее абсолютное отклонение, т.е. отклонение от многолетней средней. .

Если среднее многолетнее по данному элементу за n лет обозначим через х, а значения за отдельные годы через у, то получим формулу для вычисления среднего абсолютного отклонения (V):

.

Смысл среднего абсолютного отклонения прост. Оно показывает, насколько в среднем отдельные значения случайной величины отклоняются от средней арифметической. Чем больше V, тем больше изменчивость данной случайной величины.

При использовании среднего абсолютного отклонения V вклад малых и больших отклонений х от учитывается одинаково, что снижает ценность V как показателя изменчивости и в настоящее время он употребляется для расчетов редко.

Наиболее распространенным показателем изменчивости является среднее квадратическое отклонение  – «сигма». Сигма имеет размерность осредненного признака и вычисляется по формуле:

.

В тех случаях, когда исходным материалом является статистическое распределение (сгруппированный ряд), используется формула:

,

где - срединное значение интервала (градации); т_i – частота градации; k – число градаций.

Среднее квадратическое отклонение является параметром многих теоретических распределений.

Коэффициент вариации является относительной характеристикой, особенно в тех случаях, когда непосредственное сопоставление  (среднеквадратических отклонений) для оценки изменчивости непоказательно. Если возникает необходимость сравнения изменчивости различных рядов или отдельных частей одного ряда, сопоставление рассеивания осуществляется с помощью

.

Квадрат среднеквадратического отклонения называют дисперсией σ².

Дисперсия вычисляется по формулам для сгруппированных и несгруппированных данных.

Для простого хронологического ряда дисперсия (σ ²) вычисляется по формуле:

.

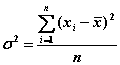Для статистического распределения (сгруппированный ряд)

.

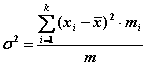Возможная точность средних значений. Какова же вообще точность многолетних средних и какую точность рационально применять для климатологических характеристик – нужны ли, например, десятые доли градуса в средних по температуре и т.д.? Абсолютно точной многолетней средней можно считать среднюю за очень длинный период, такой, что от добавления новых лет средняя практически не меняется.

Точность средних определяется обычно путем вычисления их возможных отклонений (ошибок) от средней для бесконечно длинного ряда. Эти ошибки зависят от длины взятого периода наблюдений. Эти отклонения (ошибки) средних, как и ошибки ежегодных данных вычисляются в виде среднеквадратических отклонений. Например, по широко известной формуле:

.

Из формулы делается еще один важный вывод, а именно: можно подсчитать, какой период необходим для того, чтобы средние из этого периода имели заданную точность. Для определения периода представим формулу в таком виде:

.

Например, зададим для средних температур точность 0.1°, следовательно, принимаем σ=0,1°. Тогда, зная величины σ_х , получим следующее число лет n, нужное для определения средней многолетней температуры с точностью 0.1.

Результаты вычисления показывают, что только средние годовые температуры воздуха могут быть определены из имеющихся в настоящее время рядов наблюдений с точностью до 0,1°. Несмотря на только что сделанные выводы, средняя месячная температура приводится с десятыми долями градуса. Нет ли здесь противоречия? Дело в том, что ошибки средних рассчитывались выше по отношению к бесконечно длинному периоду. Это имеет теоретический интерес и дает представление о возможных колебаниях средних в зависимости от использованного периода наблюдений. Для большинства же вопросов климатологии и для многих практических задач важно иметь среднюю не столько из очень длинных, сколько из одинаковых по длительности рядов наблюдений. Имея одинаковые по длительности ряды, можно правильно решать такие важные вопросы, как сравнение климатических условий различных районов земного шара, изменения и колебания климата и т.д.

Вертикальные градиенты температуры в свободной атмосфере (и некоторые другие величины), рассчитанные на 100 м, необходимо давать в сотых долях градуса, так как ошибка в десятых долях градуса на 100 м повлечет за собой ошибки в несколько градусов для самой температуры уже при нескольких километрах поднятия.

В других случаях десятые и сотые доли градуса являются излишними. Абсолютные максимумы и минимумы температуры принято давать в целых градусах. Эти величины, полученные по единичным наблюдениям, отличаются меньшей точностью, чем средние. Температура на поверхности почвы как средняя, так и крайняя, тоже дается в целых градусах, так как сами наблюдения отличаются небольшой точностью.

Таким образом, точность средней величины зависит от характера запросов. Например, сравнение средних месячных температур с точностью до десятых долей имеет важное значение для сельского хозяйства, для курортологии и вообще в том случае, когда имеют значения систематические различия температуры, повторяющиеся из года в год. Очень точно нужно вычислять вероятность ливня, который может размыть железнодорожную насыпь или разрушить мост данной конструкции и т.д.

В других случаях точность с десятыми долями не требуется. Например, при обслуживании аэродромов, в общедоступных климатических описаниях различных стран и районов.