Цель работы: изучить виды метеорологических (климатологических) рядов и основные климатические показатели.

 

1. Понятие о метеорологических рядах

За продолжительное время на станциях накапливается материал метеорологических наблюдений, который служит основой для составления метеорологических рядов. Метеорологический ряд – статистическая совокупность числовых значений метеорологических величин или характеристик атмосферного явления. Статистическая совокупность может быть представлена:

1. В виде простого статистического ряда (простая статистическая совокупность).

2. В виде статистического распределения (группированный ряд).

3. В виде ранжированного ряда.

В первом случае значения х_i величины х, наблюдавшиеся в момент времени t_j, обычно располагаются в хронологической последовательности (хронологический ряд). Примером хронологического ряда служат различного рода таблицы последовательных записей результатов метеорологических наблюдений (например, таблицы месячной отчетности). Метеорологический ряд, представленный в виде хронологической последовательности, имеет важное значение, так как только по хронологическому ряду возможно рассчитать различные характеристики динамики ряда (например, изменения и колебания климата), изучить закономерности изменения случайной величины во времени – от года к году, от одного десятилетия к другому десятилетию и т.д.

Одним из видов обобщения результатов многолетних наблюдений является представление метеорологического ряда в виде статистического распределения. Он состоит в группировке числовых значений метеорологических величин по определенным градациям (интервалам). Статистическое распределение записывается в виде таблицы, входами в которую являются интервалы (или середины интервалов) и численности, выражающие частоту значений данного элемента, входящих в каждый интервал:

Середина интервала.......... x_j x₁ x₂ x₃ x_k

Абсолютная частота......... m_j m₁ m₂ m m_k

Относительная частота...... p_j p₁ p₂ p₃ p_k

Численностями интервалов служат абсолютная (m_j) и относительная (p_j) частоты интервалов.

Абсолютная частота интервалов – это число случаев попадания значений метеорологических величин в тот или иной интервал.

,

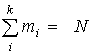где N – объем статистической совокупности (число наблюдений).

Относительная частота интервала выражается отношением числа случаев со значениями элемента, входящими в данный интервал, к общему числу наблюдений:

Метеорологический ряд в виде статистического распределения представляет обобщение результатов наблюдении и позволяет получить верное представление об основных закономерностях многолетнего режима метеорологических величин: о наиболее часто встречающихся значениях элемента и диапазоне его изменений.

При представлении группированного ряда важно выбрать размер градации. Однозначных рекомендаций по этому вопросу нет в литературе. Однако имеются некоторые эмпирические правила определения ширины интервала.

При выборе числовых градаций рекомендуется основываться на следующих положениях: 1) при группировке необходимо руководствоваться генетическими соображениями, объемом выборки и изменчивостью элемента;  2) градации не должны перекрываться; 3) не должны группироваться вблизи одной границы распределения; 4) при затруднении выбора числа градаций на основе генетических соображений необходимо использовать числовые оценки.

Одним из наиболее простых способов определения числа градаций является выражение:

,

где k – число градаций, N – объем обрабатываемой информации, lgN – десятичный логарифм N.

Установлено примерно следующее максимально возможное число градаций в зависимости от числа наблюдений:

число наблюдений (п)   30   50   100   500

число градаций (k)         7      8     10     13

Из всего объема совокупности выбирают наименьшее значение х_min.- и наибольшее значение х_max величины и определяют размер градации:

,

где i – размер градации.

С учетом асимметричности распределений при наличии известного среднеквадратического отклонения (σ) группировку рекомендуется проводить следующим образом.

1. По среднеквадратическим отклонениям с границами градаций.

2. То же по 0,5

В специальных целях может быть принята и другая последовательность результатов наблюдений. Метеорологический ряд представляется в порядке возрастания (или убывания) числовых значений членов ряда - ранжированный ряд:

.

где m – порядковый номер члена ряда; n – объем совокупности.

 

По ранжированному ряду можно вычислить (определить) интегральную вероятность (накопленную - кумулятивную повторяемость).

Для ранжированного ряда в качестве средней величины находится медиана.

Медианой называется значение, стоящее в центре ранжированного ряда, т.е. расположенного в порядке убывания или возрастания значений х_i. При этом число единиц совокупности с большим или меньшим, чем медиана, значением ряда одинаково.

Если всем единицам ряда придать порядковые номера, то номер медианы в ряду с нечетным числом «n» определяется как (n+1)/2. Например, в ряду из 81 члена номер медианы (81+1)/2=41, т.е. медианой является значение, стоящее в ряду под номером 41.

Если число членов в ряду четное, то медиану определяют как среднюю из двух центральных значений ранжированного ряда, порядковые номера которых n/2 и (n/2+l).

Так, если в ряду 80 значений, то центральными будут ранжированные значения с порядковыми номерами 80/2=40 и (80/2+1)=41.

Медиану рекомендуется определять в дополнение к средней арифметической при асимметричных распределениях. Медиана может быть определена графическим путем. По интегральной кривой распределения медиана (Me) определяется как 50% квантиль (значение метеорологической величины, накопленная вероятность которой p=0,5)

Ряды, подлежащие климатологической  обработке, могут быть составлены из средних суточных, экстремальных величин, средних месячных значений метеовеличин за отдельные годы, из средних широтных за отдельные месяцы и т.д.