В предыдущем разделе периодическая функция представлялась в виде разложения по синусам и косинусам. Почему мы не представляли эту функцию в виде ряда по периодическим функциям другого рода, например с помощью функции тангенс? Причина состоит в том, что синусы и косинусы обладают очень важным свойством – ортогональностью. Это означает, что средние значения произведений типа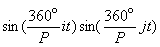 
при осреднении за весь основной период Р равны нулю, за исключением случая, когда i=j. Далее, средние 
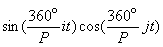за период Р равны нулю для всех i и j.
Следствием ортогональности является то, что все коэффициенты упомянутых выше гармоник могут быть определены независимо друг от друга. Иначе говоря, чтобы найти, например, A1 и B1, не требовалось решать систему всех 12 уравнений для 12 величин A и В.
Существует еще другое следствие ортогональности синусов и косинусов. Пусть мы хотим описать временной ряд с помощью единственной гармоники с периодом Р, причем сделать это так, чтобы сумма квадратов отклонений между наблюдениями и синусоидальной кривой была бы минимальной. Как рассчитать такую кривую? Оказывается, что формулы для коэффициентов А и В для членов с синусом и косинусом соответственно будут точно такими же, как выражения для A1 и B1, применяемые в гармоническом анализе. Точно так же, если бы мы хотели определить наиболее подходящую синусоидальную кривую с периодом P/2 мы получили бы те же формулы, что для A2 и B2.
Ортогональные функции применяются не только для описания периодического временного ряда. С ортогональными функциями мы снова встретимся, когда речь пойдет о пространственном ряде. Эти функции определяются более широко: ряд функций fn (х, у, ...) ортогонален, если среднее значение (осредненное за какой–нибудь определенный интервал х, у и т. д.) произведения fn(x, у, ...) fm(x, у, ...) равно нулю, за исключением т = п. При m = n мы оперируем средним значением квадрата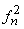 
(x, у, …), которое, конечно, не равно нулю и является, как правило, известной величиной. (Это определение иногда обобщается следующим образом; 
, где g(x, у) – произвольная весовая функция.)
Фактически функции часто выбираются так, чтобы сумма их квадратов равнялась единице; в этом случае функции называются ортогональными и нормированными или сокращенно – ортонормированными. Функция
является примером ортонормированной функции.